In the final installment of this three part series, we are going to use our results from the previous two posts to construct a fully automated variable leverage ETF. In part one, we derived the optimal leverage ratio for maximizing returns and in part two we applied the ARMA and GARCH models to forecast returns and volatility, respectively.
The ETF we are going to build will take variable leverage with a minimum leverage of 1 and a maximum leverage of 3. This means that the leverage ratio we will be assuming will deviate considerably from what is optimal. The reason for this is twofold: 1) many investors don't want to short the market, regardless of what our model says, preferring a baseline of pure beta exposure, and 2) the SEC rejected an application for the creation of a 4x S&P 500 ETF, so it would be unlikely that a higher leverage ratio could be assumed, at least in an ETF wrapper. If one was instead obtaining leverage directly through futures, -20x to 20x leverage could be taken.
Right now, we have two components, $\text{E}(r_m)$, the expected monthly return generated from our ARMA model, and $\text{E}(\sigma_d)$, the expected daily volatility from our GARCH model. First off, we need to forward fill our monthly return data, in order to generate return data for everyday. We forward fill instead of back fill in order to avoid lookahead bias. Also, because our ARMA model is forecasted the future one month expected return, we convert our daily volatility into monthly variance: $21\text{E}(\sigma_d)^2$. So our raw leverage ratio becomes:
\[l = \frac{\text{E}(r_m^{\text{fill}})}{21\text{E}(\sigma_d)^2}\]Let's look at graph of our leverage ratio over time to get a sense of what we're dealing with:

Oof, most investors won't be happy with that! Not only is our optimal leverage calculation taking huge short and long positions, but it's changing the direction of the portfolio very frequently. We want to smooth out the changes in leverage as well as constrain the amount taken between 1 and 3. In order to do this, we apply the following transformations on the time-series:
-
First, if the leverage ratio is less than 1 at a time-point, we set it to 0.
-
In order to constrain the values, we then add $e$ and logscale it. This should give us values approximately between 1 and 3.
-
To smooth the leverage, we apply an exponential rolling window, with an $\alpha$ of 0.05.
-
If any values are above 3, we set them to 3.
Below is the full transformation:
\[f(x) =\begin{cases} x &\text{if }x > 1\\ 0 &\text{else}\\ \end{cases}\] \[\sum_{t=1}^n \min(\text{EWM}_{\alpha=0.05}[\log(f(x_t)+e)],\,3)\]Consider the graph of adjusted leverage:
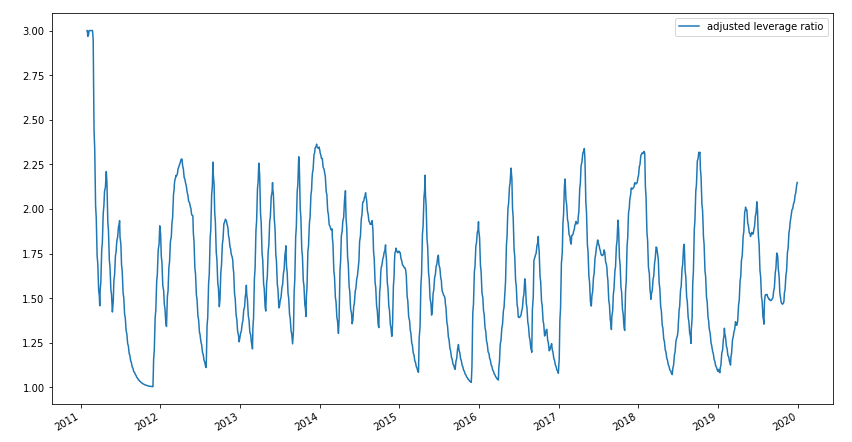
Though we're significantly deviated from what the optimal leverage is, our adjusted leverage looks a lot more reasonable. The transitions are smoother and the values are bounded between 1 and 3, as desired. Now we simply multiple the leverage ratio by the returns of the S&P 500 and we have our strategy! This is the moment of truth, let's look at a graph of the returns of the S&P 500, the returns of our ETF, and the leverage ratio:
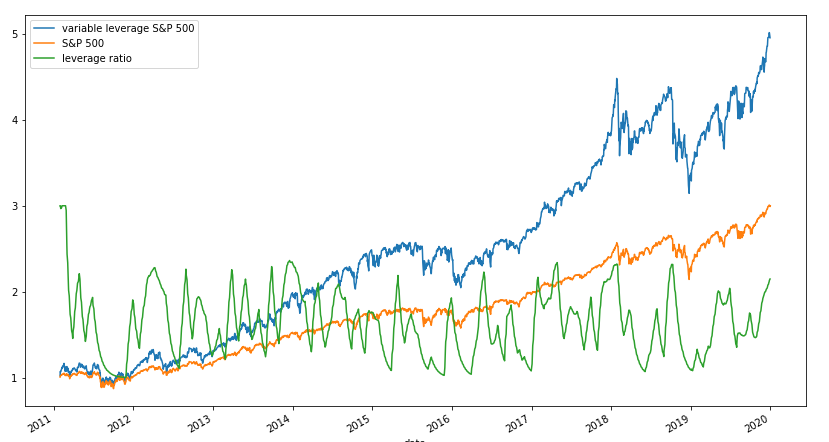
Not bad! Our ETF is behaving as expected: taking on more and more leverage during bull runs and reducing exposure when the market drops. The leverage ratio fluctuates between 1 and 2 due to our smoothing factor, though more risk could be taken by choosing a greater $\alpha$ value.
Conclusion
At long last, we've reached the end of this series. We've talked about investors, mostly irrational, aversion to holding leveraged ETFs over a long period of time, derived the optimal leverage ratio to maximize returns, created models to forecast returns and volatility, and used all of this to create a variable leverage ETF. Could such a product be brought to market, and would investors be interested? Can investors be convinced to hold any product that isn't just vanilla beta? I'm not sure, but it is certainly an interesting opportunity. No product on the market fulfills this niche, if there is even one to exploit. I hope you enjoyed this series as much as I enjoyed researching and writing it. Though we did succeed in creating a rudimentary model, so much more work could be done on it. I believe that a variable leverage product could have great potential in the retail space, especially now that vanilla beta has been completely commoditized. New ETF ideas that are "beta plus" not only have the potential to deliver value to investors, but also could command much higher fees.
You can check out the notebook here. Feel free to play around with any and all parameters.