Risk parity is a popular method of investing that aims to outperform the traditional 60/40 equity/bond portfolio by equalizing the risk of the bond portion with that of the equity part of the portfolio and then leveraging up the portfolio to hit the desired risk target. Using the covariance, and volatility of the components, we can generate a portfolio and leverage ratio for a given level of desired risk. This works for two reasons: bonds have a low or inverse correlation to equities and they generally have superior risk-adjusted returns as well, and combining low correlation assets allows us to lower the volatility of the portfolio. Bridgewater and Ray Dalio pioneered this approach in the 90s with the introduction of his now famous All Weather fund.
The appeal of this approach is obvious compared to the 60/40 portfolio: by setting a volatility target, we stabilize our risk throughout different market regimes. This is an attractive property for investors who might otherwise choose a 60/40 or even all equity portfolio; they can sleep well knowing an appropriate level of risk will be taken, regardless of the market. Well, in this post, we're going to take a less sensible approach and instead of equalizing the risk in our portfolio, we're going to leverage up the equity component (representing almost all of the risk of the portfolio) and use the bonds to generate yield.
Risk Imparity
The intuition behind this approach is pretty straightforward: we want to take on leverage with equities and cancel out the leverage by choosing an appropriate weight. For example, if we purchased a 2x bull leveraged S&P 500 ETF such as SSO, we would choose an appropriate weight to cancel out the leverage, 0.5 in this case. If we kept the rest of the money in cash, the return of the portfolio would only be slightly worse than that of the S&P 500, due to the 0.90% expense ratio we pay. If we didn't have to pay an expense ratio, the return streams would look identical besides for perhaps some marginal tracking error. But if we instead invested the rest of the money in a low risk investment, such as investment grade bonds, we would earn yield on the money and diversify our portfolio. As long as the bonds contribute more profit than the cost of the expense ratio, the strategy should beat the vanilla index. Below is the strategy in full:
-
Our portfolio will consist of two assets, UPRO, a 3x leveraged S&P 500 ETF, and LQD, an investment grade bond ETF.
-
Each day, we will rebalance so that 1/3 of our portfolio is allocated towards UPRO and 2/3s towards LQD.
Let's look at the returns against the S&P 500 between 2009-06-26 and 2020-07-28 (we choose the beginning date because UPRO was at the beginning of 2009 and the data only became available for it at the start date):
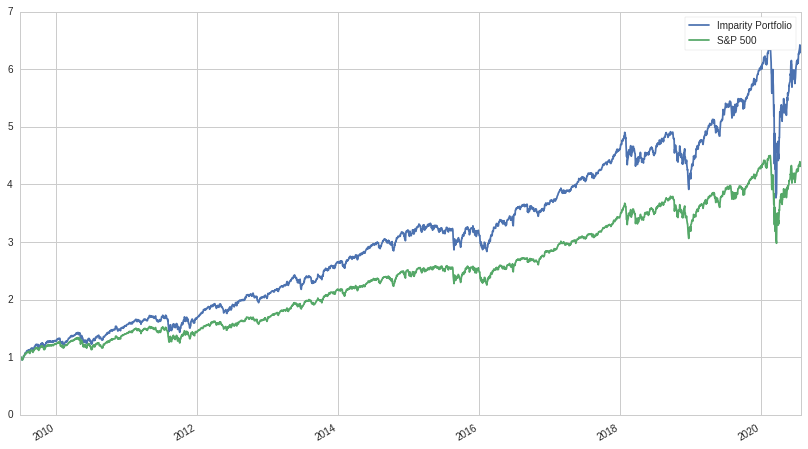
Not bad, let's look at a table of metrics:
| Metric | Portfolio | S&P 500 |
|---|---|---|
| Ann. Rets | 18.1% | 14.1% |
| Ann. Vol | 18.4% | 17.4% |
| Ann. Sharpe | 0.98 | 0.81 |
| Beta | 1.02 | 1.0 |
The results are pretty impressive for such a simple strategy: better Sharpe ratio, comparable beta, and a 4% better annualized return, with only slightly higher volatility. One problem however, is apparent: if the traditional negative correlation between bonds and equities starts to break like it did during the start of Coronavirus, the portfolio takes a major hit, performing worse than the S&P 500. In order to confirm this, let's look at LQD alone:

And indeed, even investment grade bonds collapsed during the start of Coronavirus. But what about the Great Recession, how did the strategy perform then? We don't have real data from that time-period, but we can synthetically generate a comparable return stream by just multiplying SPY by 3. This of course won't take into account the expense ratio of UPRO and the tracking error, but the results should still be pretty similar. Let's take a look:

Unlike during Coronavirus, The strategy held up pretty well during the crash of '07-08, returning approximately the same as a pure S&P 500 portfolio. This might suggest a regime change in bond/equity correlation or a temporary blip that isn't indicative of future correlation.
Conclusion
Though there are risks associated with this strategy not present in a pure S&P 500 portfolio, in most market environments, this approach delivers a better risk-adjusted return without taking on any additional market risk. Another benefit of the strategy is its simplicity: by using only two different ETFs, a retail investor can manage the strategy with minimal effort. investor could also adjust the rebalancing period to weekly or monthly in order to reduce the complexity and transaction costs. The strategy can also be modified by adjusting the type of bond for the portfolio: more risk-averse investors could stick with short to medium term Treasury notes while higher octane ones could substitute in junk bonds or other alternative investments.
Thanks for reading, hope you enjoyed this post. Click here for the Quantopian notebook used. Seeing that this strategy is pretty trivial, if anyone could help me in locating prior literature about it, I would be most appreciative. Email me at sturm@cryptm.org if so.