This post is going to be a little different from usual; instead of markets, we're going to look at a video game, namely, Counter-Strike: Global Offensive (CS:GO). CS:GO, like most great games, is easy to learn but deceptively hard to master. For those at are unfamiliar with the game, we'll give a quick overview below.
CS:GO is a competitive zero-sum game in which two teams of 5 players each try to win rounds. The first team to 16 points wins the game. The game is asymmetric as there are two distinct sides: the terrorists (T-side) and counter-terrorists (CT-side). After 15 rounds, each team switches sides. The goal of the T-side is to either eliminate all CT players or to plant a bomb and have it explode before the CT-side can defuse it; the CT-side wins the round if kill all the players on the T-side before the bomb is planted, if they defuse the bomb, or if time runs out on the round. this asymmetric rule-set implies that the CT-side can lose a round even if they kill all the opposing players, while the T side cannot lose if they eliminate all CT players.
In order to get a better idea of the structure of the game, let's look at a top-down perspective of one of the most famous and iconic maps, Dust2:
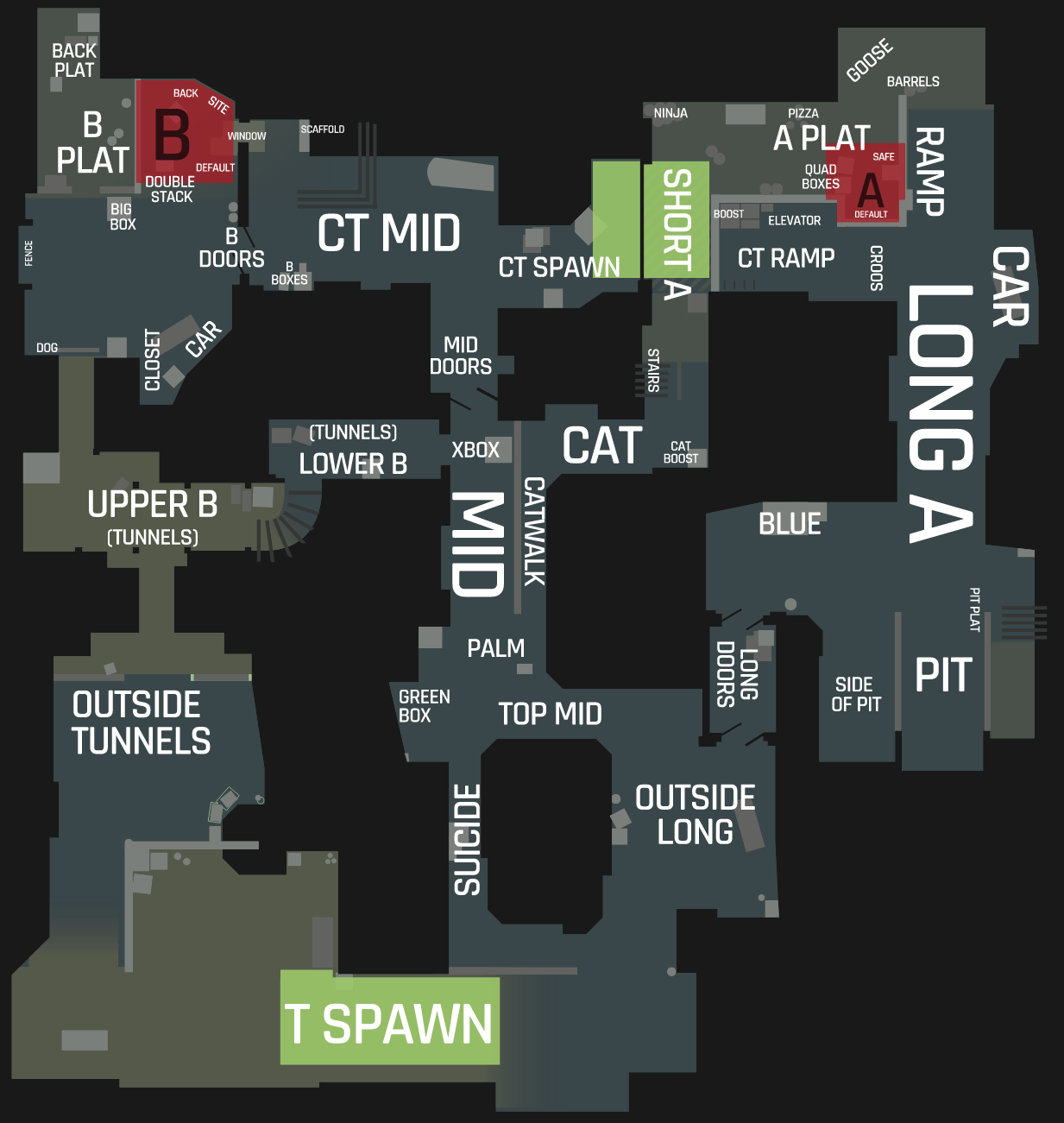
T-side starts the game in T-spawn and must plant their bomb at one of two locations: B-site or A-site, designated by the red areas on the map. the CTs start off in CT spawn and must try and defend these two sites. If T-side manages to break the CT defenses and plant the bomb, the remaining players on CT try and retake the bombsite (either A or B) and defuse the bomb before it explodes.
Because of the asymmetric nature of the game, I thought it would be interesting to analyze how much a kill effects the game for each side. To start off with, we'll first look at the situation where the number of players on each side is equal.
Even Match-ups
First up, let's look at the so-called even match-up, where there are an equal number of players on each team: 5v5, 4v4, etc. Using over 400,000 rounds of match data from mid-2018 (click here for the original dataset), we aggregate all rounds with even match-ups and the side that wins. From this, we can calculate a cumulative win probability for each match-up:

From the above graph, it's seems that the T-side enjoys a significant advantage. Even when the match starts, the CT-side has a less than 50% of winning the round and as trades are made (a situation where each team loses a player), the advantage the T-side has only goes up. But is this significant? Let's look at a table of CT-side win rates and their associated p-value:
| CT win rate | p-value | players |
|---|---|---|
| 0.48729 | 2.67482e-55 | 5 |
| 0.469768 | 1.17974e-151 | 4 |
| 0.455098 | 3.84482e-237 | 3 |
| 0.439982 | 1.52963e-319 | 2 |
| 0.430299 | 2.35914e-282 | 1 |
It's clear from the minuscule magnitude of the p-values that we can reject the null hypothesis, namely that each even match-up is fair: a 50% chance of each side winning the round.
All Match-ups
Now that we've established that even when each side has the same number of players the T-side has an advantage, let's consider all the possible combinations. Clearly a situation when 5 CTs are up against 4 Ts is not a fair fight (We might assume that CTs have the advantage), but unfair is it? After crunching the number for each permutation, we get the following graph:
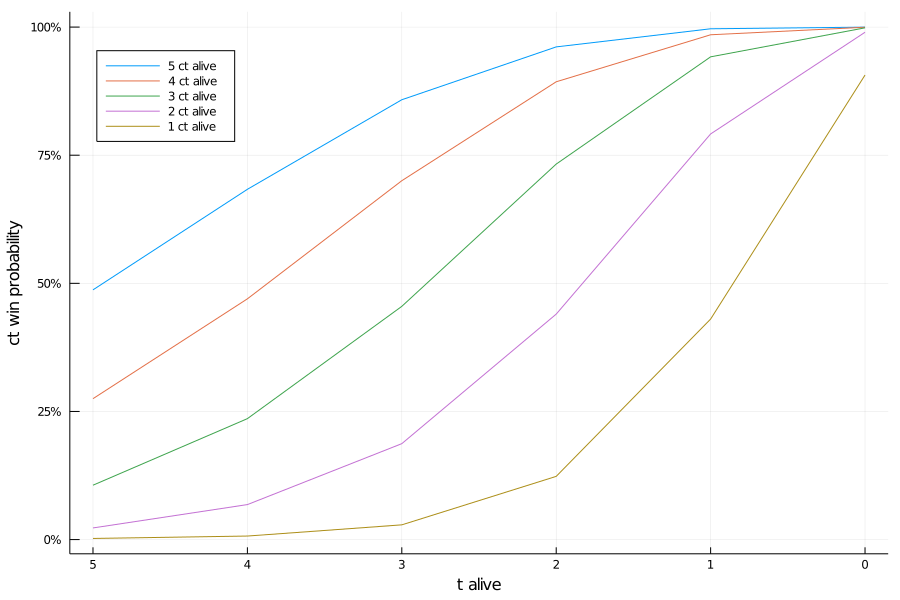
Interesting! When the CTs have close to the number of players as T-side, the first kills make the most difference. A 5v5 for the CT side gives them a 48% chance of victory, but netting the first kill shifts the odds considerably to 68%. When the difference is large, the final kills have the highest percentage chance, as the chance of the CT-side winning is so low to start off with. Below is a graph of the exact figures:
| 1 CT | 2 CT | 3 CT | 4 CT | 5 CT | # T alive |
|---|---|---|---|---|---|
| 0.00218907 | 0.0227307 | 0.106122 | 0.274956 | 0.487288 | 5 |
| 0.00689667 | 0.0682988 | 0.235994 | 0.469768 | 0.683482 | 4 |
| 0.0287596 | 0.187184 | 0.455091 | 0.70026 | 0.858241 | 3 |
| 0.123364 | 0.439972 | 0.732706 | 0.893306 | 0.961373 | 2 |
| 0.430299 | 0.7915 | 0.941975 | 0.985024 | 0.9967 | 1 |
| 0.906434 | 0.989945 | 0.998562 | 0.999731 | 0.999873 | 0 |
Conclusions
I know little about professional CS:GO strategy and the data isn't taken from professional games, but we can quickly infer a couple things from the data:
- T-side wants to trade down as much as possible, CT never wants to trade.
- CT-side needs to be play very conservative, maximizing the number of players on their team that are alive.
- T-side wants to play in a very aggressive style in order to take map control and trade.
Anyways, this has been a fun little post to write, I hope you enjoyed it! Click here to view the GitHub project.